
We use the formulas expressing Cartesian in terms of spherical coordinates (setting ρ = a since (x,y,z) is on the sphere): (10) x = asinφcosθ, y = asinφsinθ, z = acosφ. Create a new workbook with three columns X, Y and Z. 9) is represented by the ordered triple (ρ, θ, φ) where.

Theorem (Cartesian-cylindrical transformations) The Cartesian coordinates of a point P = (r,θ,z) are given by x = r cos(θ), y = r sin(θ), and z = z. Set up an integral for the volume of the region bounded by the cone z = √3(x2 + y2) and the hemisphere z = √4 − x2 − y2 (see the figure below). Solution: Z Z Z E xyzdV = Z 10 0 Z z 0 Z y 0 xyzdxdydz= Z 10 0 Z z 0 1 2 圓zdydz = 1 8 Z 1 0 0z5dz= 1 48 106 6. This is the distance from the origin to the point and we will require ρ ≥ 0 ρ ≥ 0. Some surfaces, however, can be difficult to model with equations based on the Cartesian system. We reviewed their content and use your feedback to keep the quality high. 5makes it clear that the polar coordinate rof the point (x y) is ˆsin˚, and that z= ˆcos˚. Measure the angle from the positive … The -coordinate describes the location of the point above or below the -plane. Suppose that in a coordinate system whose origin is at the center of the planet, the magnetic field strength is given by I(x,y,z)=4xz+4yz+7. Solution: In spherical coordinates 3 Spherical Coordinates The spherical coordinates of a point (x y z) in R3 are the analog of polar coordinates in R2. This is not a useful method for recording a position on maps but is used to calculate distances and to perform other mathematical operations.
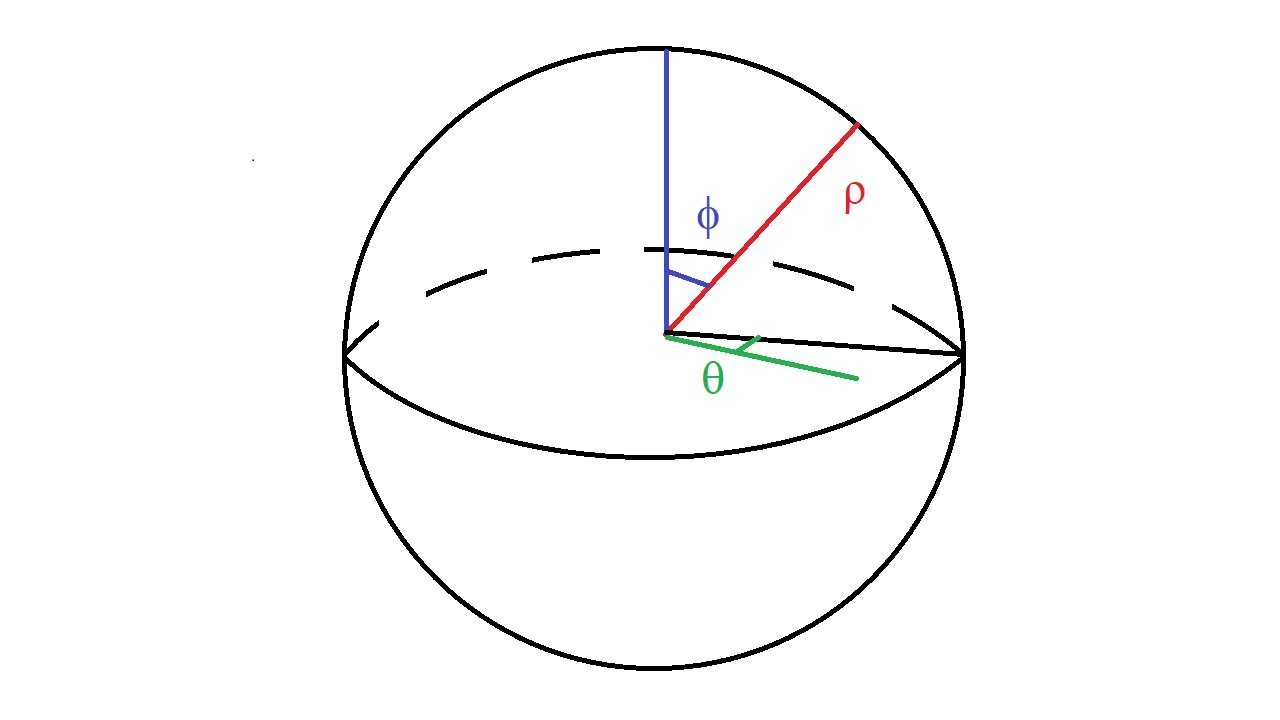
2: The Pythagorean theorem provides equation r2 = x2 + y2. The coordinate change transformation T(r z) = Specifically, the cartesian coordinates ( x,y,z) of a point P are related to the spherical coordinates ( r,f,q) of P through two right triangles. To derive the line element, consider an infinitesimal displacement (dρ, dφ, dz) in cylindrical polar coordinates.Spherical coordinates x y z. In cylindrical polar coordinates, a point in space is represented by (ρ, φ, z), where ρ is the radial distance from the z-axis, φ is the azimuthal angle (0 ≤ φ ≤ 2π), and z is the height along the z-axis. This is the volume element in spherical polar coordinates. This volume can be represented as the product of the infinitesimal lengths along the r, θ, and φ directions:ĭV = dr * (r * dθ) * (r * sin(θ) * dφ) = r^2 * sin(θ) * dr * dθ * dφ
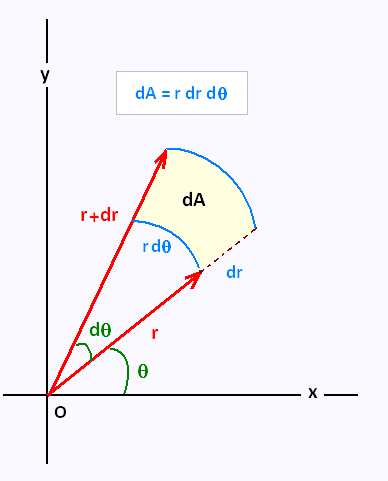
To derive the volume element, consider an infinitesimal volume dV enclosed by the surfaces r, r + dr, θ, θ + dθ, φ, and φ + dφ. This is the area element in spherical polar coordinates. This area can be represented as the product of the infinitesimal lengths along the θ and φ directions:ĭA = (r * dθ) * (r * sin(θ) * dφ) = r^2 * sin(θ) * dθ * dφ To derive the area element, consider an infinitesimal area dA on a sphere of radius r. This is the line element in spherical polar coordinates. Substituting the expressions for dx, dy, and dz, and simplifying, we get:ĭs^2 = dr^2 + r^2 * dθ^2 + r^2 * sin^2(θ) * dφ^2 Now, the square of the infinitesimal line element ds^2 in Cartesian coordinates is given by: The corresponding infinitesimal displacements in Cartesian coordinates are:ĭx = dr * sin(θ) * cos(φ) - r * sin(θ) * sin(φ) * dφ + r * cos(θ) * cos(φ) * dθĭy = dr * sin(θ) * sin(φ) + r * sin(θ) * cos(φ) * dφ + r * cos(θ) * sin(φ) * dθ

To derive the line element, consider an infinitesimal displacement (dr, dθ, dφ) in spherical polar coordinates. In spherical polar coordinates, a point in space is represented by (r, θ, φ), where r is the radial distance from the origin, θ is the polar angle (0 ≤ θ ≤ π), and φ is the azimuthal angle (0 ≤ φ ≤ 2π).


 0 kommentar(er)
0 kommentar(er)
